这应该是李宏毅机器学习入门基础概念的最后一篇了,后面就因为偷懒◑﹏◐开学去读论文,学习经典的深度学习模型就没写了。其实逻辑回归是构成深度学习神经元的激活函数,虽然说为了防止梯度爆炸和梯度消失,现在普遍使用的是Relu,但其重要性还是无与伦比。
概述
虽然逻辑回归(Logistic Regression)被称为回归,但它一般用于解决分类问题。为什么叫逻辑回归呢?因为在整个方法中对输入$x$我们采用线性模型$z=\omega^Tx+b$,线性模型可以进行回归学习,如果处理的是二分类问题,我们规定输出$z={0,1}$,所以叫逻辑回归。
逻辑回归实现过程
由概述我们已知知道逻辑回归是采用线性模型,假设我们现在要解决二分类问题。那怎么将模型$z=\omega^Tx+b$映射到输出$z={0,1}$呢?这时候就要利用我们在Classification最后由贝叶斯公式推导出来的$P_{\omega,b}(C_1|x)=$Sigmoid函数$\sigma(z)=\frac1{1+e^{-z} }$,具体做法如下。
建模(找未定参函数)
建模的过程就是找出一系列参数未定的函数列。对于二分类问题,我们的想法是通过与$\sigma(z)$函数相等的后验概率$P_{\omega,b}(C_1|x)$来进行判别,如果后验概率$P_{\omega,b}(C_1|x)$大于0.5,则属于类别$C_1$,小于0.5则属于类别$C_2$。所以整个模型表达式为
$$ f_{\omega,b}(x)=P_{\omega,b}(C_1|x)=\sigma(z) $$
由在Classification中的描述可知,$z=\omega\cdot x+b$($\omega, x$都是列向量),所以对于上式,$\omega,b$是未定的参数。$f_{\omega,b}(x)$是由这两个未定参数组成的函数列。
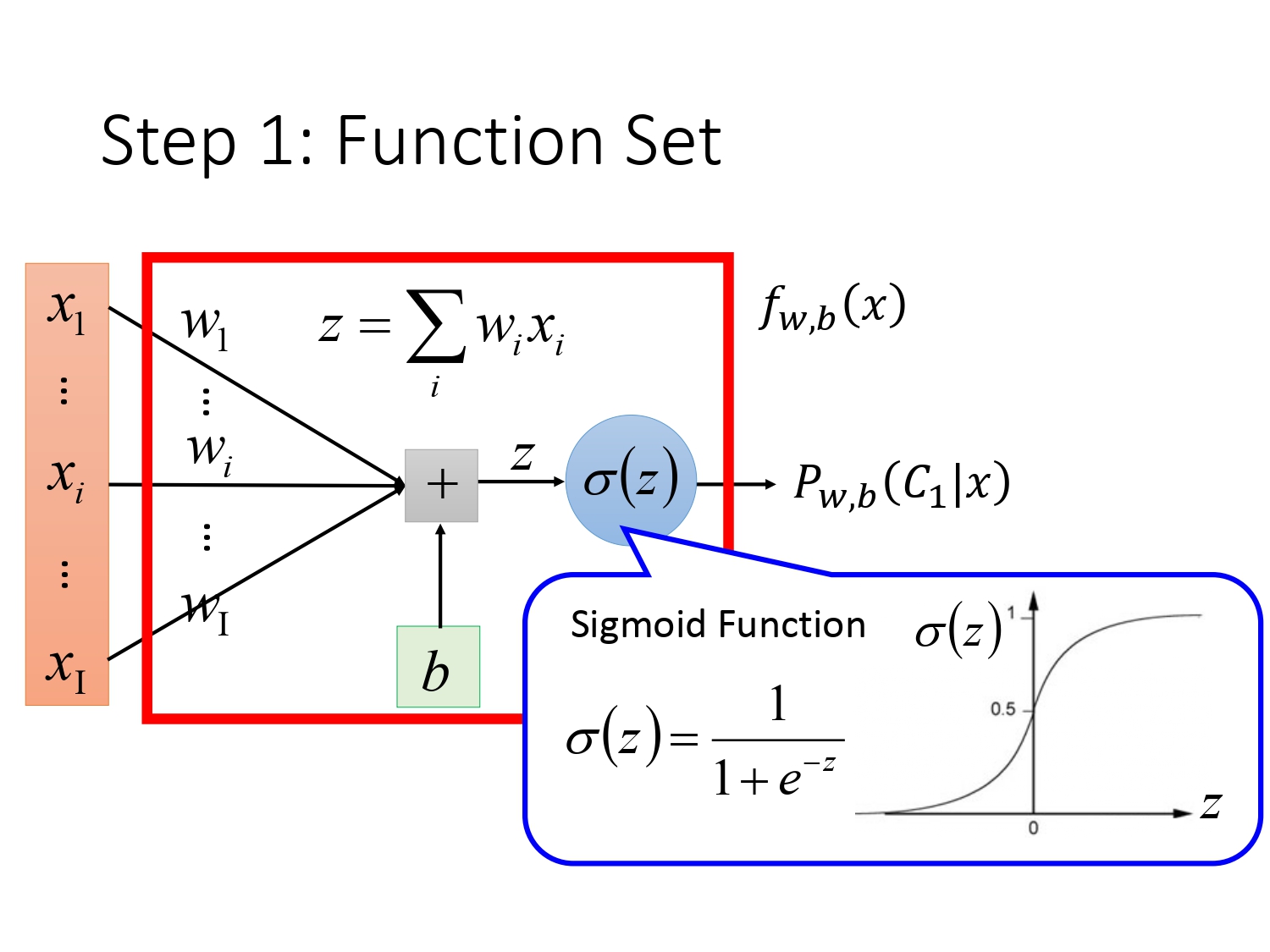
如果我们把整个模型画出可视化图的形式,结果如下所示。
找评价函数
确定模型后,我们需要定义一个判断模型好坏的评价标准,目前为止的评价函数有损失函数和似然函数。目前只有定义了损失函数(Loss Function)或者似然函数(Likelihood Function),我们才能用各种求最优解的方法去求出使得损失最小或者似然函数最大的参数。
在逻辑回归中,不妨我们先用似然函数去作为评价标准。假设现在我们现在处理二分类问题,训练集是已知分类的$N$个样本点,利用上述模型和独立事件的最大似然估计的方法,我们可以得到似然函数$L(\omega,b)$的表达式如下。

其中设$\omega^*,b^*$是使得似然函数值最大的参数,解函数为$\omega^*,b^*= \underset{\omega,b}{\operatorname{arg,max}L(\omega,b)}$,直接求最大解不好求,我们可以改成求最小值的形式为$\omega^*,b^*= \underset{\omega,b}{\operatorname{arg,min}}-lnL(\omega,b)$,类别$C_1$我们用1标注,类别$C_2$我们用0标注。则似然函数$L(\omega,b)$的每一项都可以化成下面的结果。
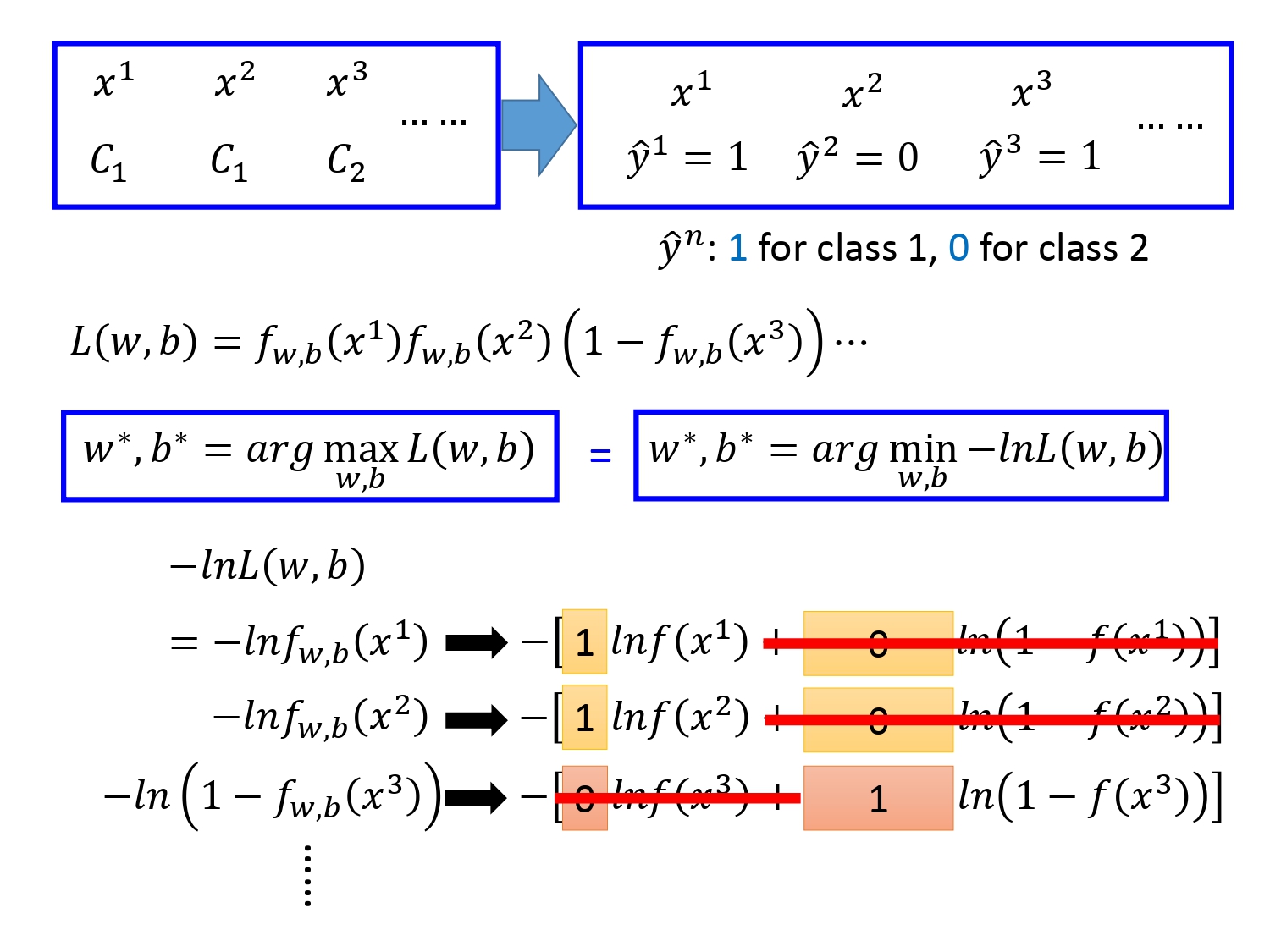
(注:图中右上角的标注错误,应该是$\hat y_1=1,\hat y_2=1,\hat y_3=0$)
交叉熵
那为什么我们要转化成对数加负号求最小值的形式计算解函数?因为取对数加负号后,可以转化为《信息论》中常见的量——熵(entropy)。为什么要转化为熵呢?因为熵是用来系统的混乱程度,熵值越大,代表系统越混乱,系统里所含的样本种类数越多;熵值越小,系统越纯,系统里面的样本种类数越单一。
熵的数学定义为$H(x)=−∑_{i=1}^np(x_i)log(p(x_i))$;其中,$p(x_i)$为事件$X=x_i$的概率,$−log(p(x_i))$为事件$X=x_i$信息量。
交叉熵的定义
根据熵的定义我们知道熵可以通过自身的概率分布,衡量自身的混乱程度。那对于两个不同的分布$p,q$,使用熵的定义去衡量它们之间的混乱程度,也就是它们之间的差异,可得到交叉熵的定义为
$$ H(p,q)=-\sum_x p(x)ln(q(x)) $$
其中交叉熵值越大,代表两个分布差异很大,交叉熵值越小,代表两个分布越相似。

对应到机器学习中,可以用交叉熵作为损失函数,假设分布$p$表示真实的分布,分布$q$表示训练后的模型预测标记分布,此时交叉熵可以衡量二者的差异性,交叉熵值越小,去负号去指数得到的似然函数的值越大,可求得最优解。
上图中划蓝线的式子代表的是两个伯努利分布(二项分布)的交叉熵。
找评价最好的函数
我们已经知道可以用两个不同分布的交叉熵去作为损失函数去衡量函数好坏。所以我们的任务是求出使得交叉熵的值最小的$\omega,b$,以下使用梯度下降的方法求解。(梯度下降具体的做法参照Regression)
下图是$lnf_{\omega,b}(x^n)$对$\omega_i$求偏导的过程。
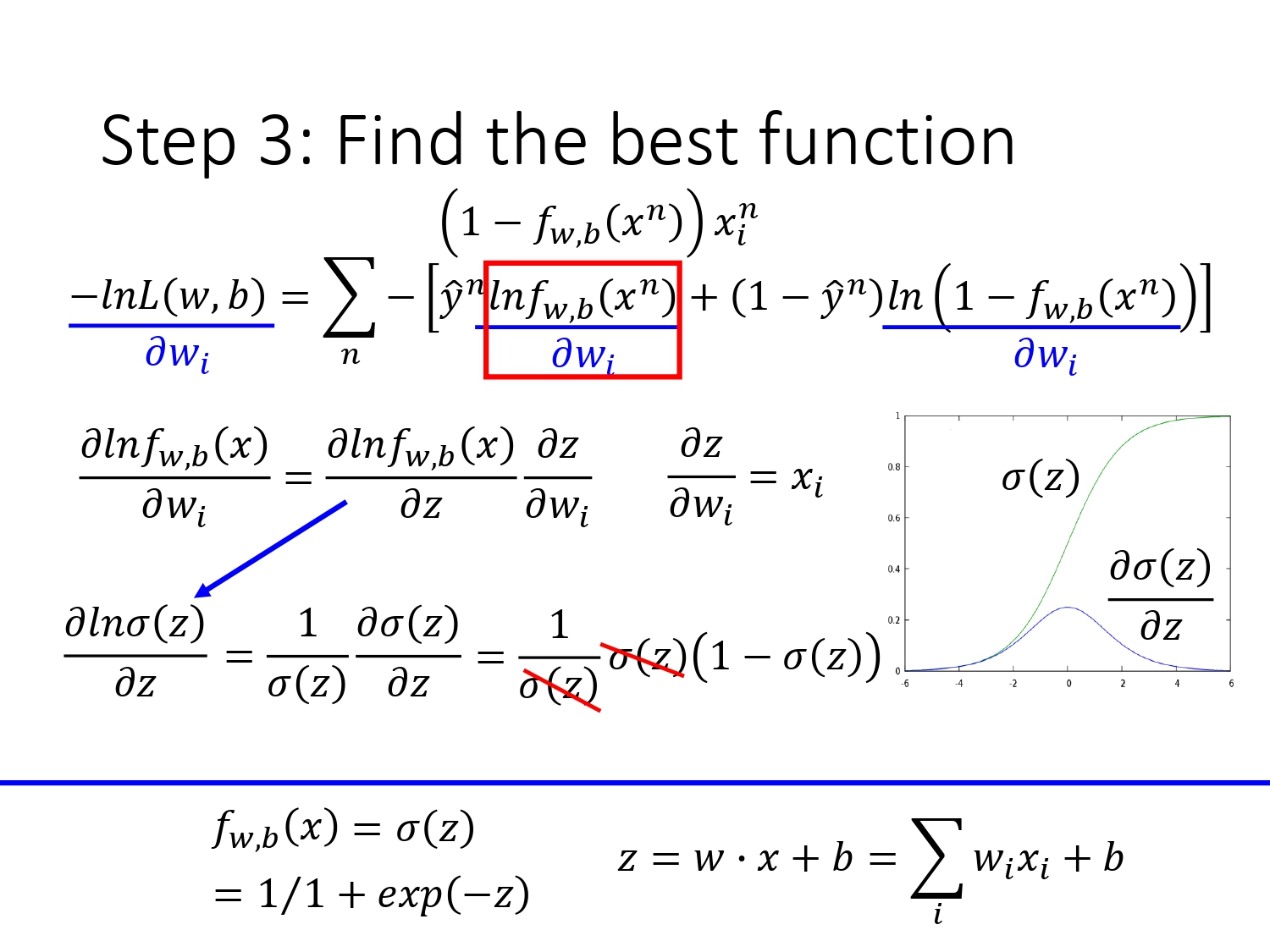
以下是$ln(1-f_{\omega,b}(x^n))$对$\omega_i$求偏导的过程。

将两项求偏导的结果加起来化简如下。

可以得到$\omega_i$更新为$\omega_i-\eta\sum_n-(\hat y^n-f_{\omega,b}(x^n)x_i^n)$。其中$\eta$为学习率。
逻辑回归和线性回归作比较
两者的对比图如下所示。

可以看出,两种回归的$\omega_i$的更新是一样的,不同的是,线性回归的目标函数可以是任意值,输出也可以是任意值,逻辑回归的目标函数是0或1,输出是介于0到1的值。并且线性回归的损失函数采用的是平方误差,而逻辑回归采用的是交叉熵。那为什么逻辑回归不采用平方误差作为损失函数呢?
其实损失函数只是个人为定义评价模型好坏的标准而已。不同的标准各有优劣,但是并不冲突,所以逻辑回归当然可以利用平方误差得到损失函数。但是可能存在以下问题。如果从分类问题的角度去解释,由下图可知,如果我们分类的目标值$\hat y^n=1$,当我们的预测值在距离目标很近($f_{\omega,b}(x^n)=1$)或是很远($f_{\omega,b}(x^n)=0)$时,似然函数$L$关于$\omega_i$的偏导都是0,换言之,当预测值在距离目标值很远的地方时,可能陷入局部最优解而不进行参数的更新或者更新很慢。

如果我们分类的目标值$\hat y^n=0$,同样会存在上述问题,具体过程如下。

如果从数学的角度解释,是因为通过最小二乘法得到的平方损失函数是非凸的,而对数似然函数是凸函数。二者的图像如下所示。
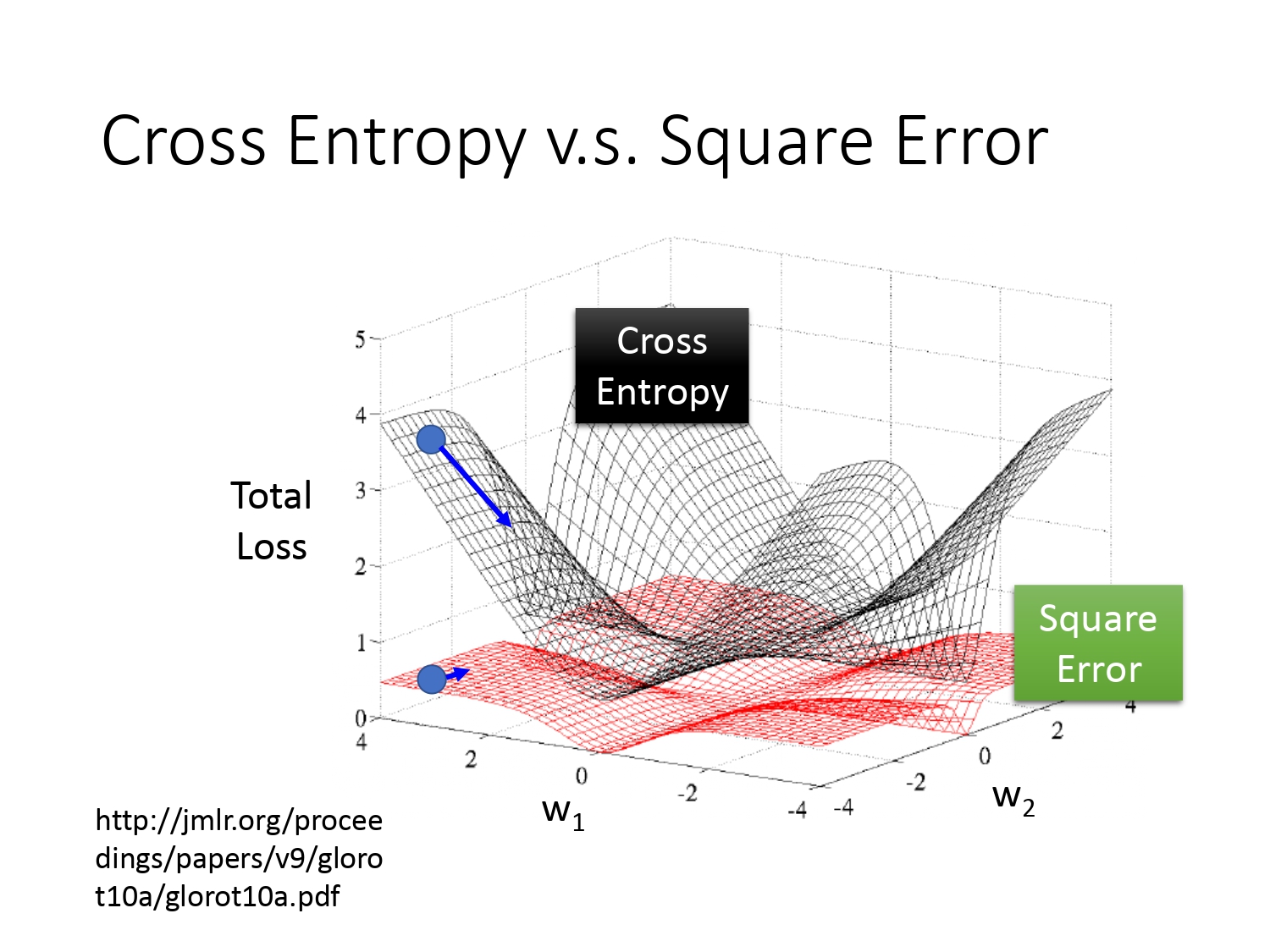
可见如果是交叉熵,在预测值距离目标越远,微分值就缩小,就可以做到距离目标越远,更新参数越快。而平方误差在距离目标很远的时候,微分值也可能非常小,这会造成移动的速度非常慢,效果较差。
还记得为什么在线性回归中我们不用担心陷入局部最优解的问题而选择平方误差作为损失函数吗?因为线性回归中,我们的损失函数$L$根本没有局部最优解。(因为无论是单变量还是多变量的线性回归,损失函数$L$都是凸函数。)
判别模型和生成模型作比较
逻辑回归的方法就属于判别模型,就是通过$\sigma(z)$函数建模,通过构造对数似然函数作为评价函数,再利用梯度下降的方法直接求解最好的$\omega,b$。如果是生成模型,要已知或者先假设训练数据服从某一分布(像上节在Classification中的概率生成模型中假设原数据服从高斯分布),再通过最大似然估计求出最好的参数(高斯分布的参数是$\mu^1,\mu^2,\Sigma$,再通过训练分类样本数$N_1,N_2$等参数求解得到最好的$w,b$。)所以对于判别模型和生成模型,它们得到的最好的$\omega,b$显然是不一样的。

如果我们使用逻辑回归对宝可梦的水系和一般系的作分类,只用两个特征的话,和之前生成模型的方法对比,效果如下。
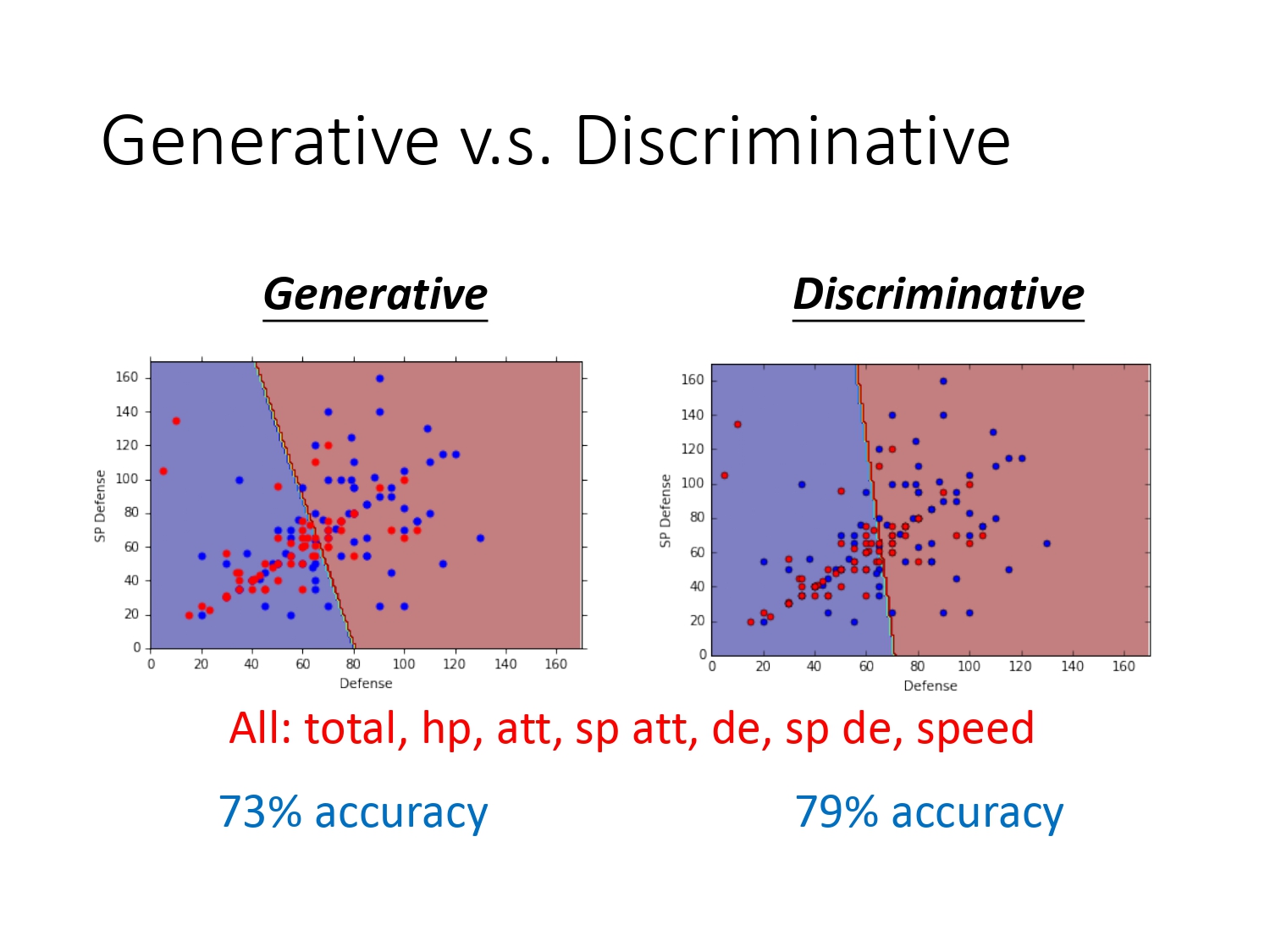
只考虑两个特征效果确实也不怎么好,如果我们考虑了所有的7个特征,准确率由73%提高到了79%。所以判别模型的效果比生成模型的要好。那判别模型的方法一定会比生成模型要好呢?
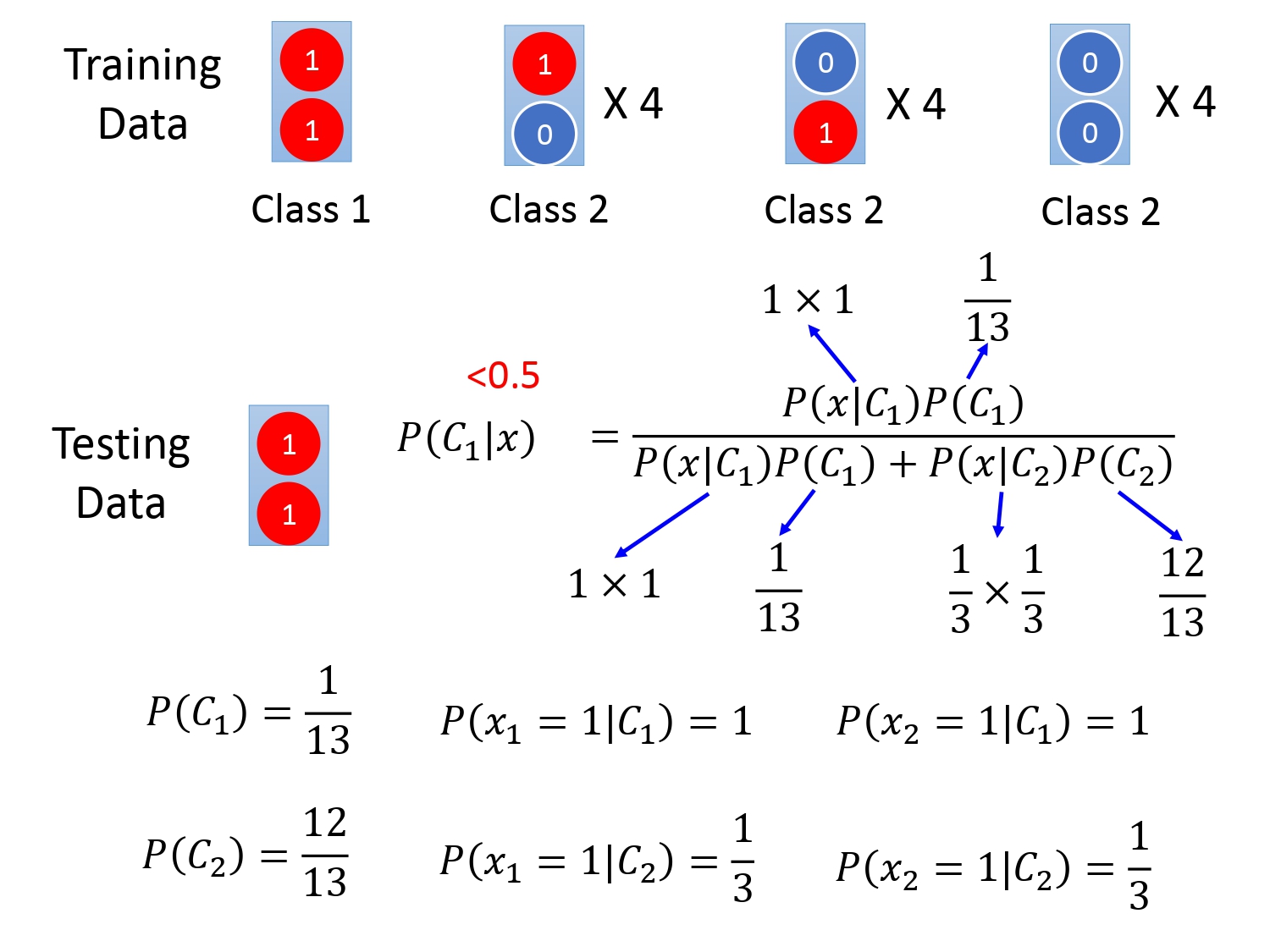
以下举个例子来说明,下图中有13组数据,除了(1,1)是类别1外,其他都是类别2。

然后如果我们新来个测试数据(1,1),毫无意外我们都认为是类别1,但是如果我们选用生成模型——朴素贝叶斯分类器(Naive Bayes Classifier)(假设问题的输入有$K$个特征,并且它们之间都是统计独立,最终先验概率的求解为各个特征的概率相乘。)进行判别,结果会怎样呢?
为使用贝叶斯公式,我们先求出贝叶斯公式的四个先验概率,再带入贝叶斯公式,求得的结果$P(C_1|x)$是小于0.5,所以分类器将它判断为类别2,这和我们的判断恰好相反。为什么使用生成模型会造成这种结果呢?
因为生成模型在进行判断前对我们的数据做了假设,假设它来自于某个概率模型(本例就是朴素贝叶斯分类器),在数据量不大的情况下进行“脑补”,当“脑补”这个模型的基础上产生足够多的数据的话,(1,1)属于类别2的概率更大,之所以我们看到(1,1)属于类别1,是因为训练的数据不够多。
那生成模型中的“脑补”算是一件好事吗?在数据量不多的情况下,“脑补”确实是必要的。那生成模型的优点有哪些呢?
对于训练数据很少或者训练集中含有噪声点时,使用生成模型往往更好,因为判别模型没有自己的假设,受数据影响较大。当数据量越来越多时,使用判别模型的$Error$会越来越小。使用生成模型还可以将先验和类相关的概率从不同的来源估计。比如说语音识别,我们可能直观会认为现在的语音识别大都使用神经网络来进行处理,是属于判别模型;但实际上整个语音识别是生成模型。所以还是需要算一个先验概率——某句话被说出来的概率,但我们估计某句话被说出来的概率不需要声音数据,只需要网络上爬很多的句子,就能计算某句话出现的几率。
Softmax回归
普通的逻辑回归只能解决二分类问题,对于多分类问题,我们对逻辑回归进行改进提出了Softmax回归。关于Softmax回归的原理,可参考《Pattern Recognition and Machine Learning》Christopher M. Bishop 著 ,P209-210。以下我们只介绍Softmax回归的用法。
假设我们现在有三个类别$C_1,C_2,C_3$(记为$ C_i(i=1,2,3)$),它们被预测时都有回归中最好的权值$w_i$和偏置$b_i$,假设现在有测试样本$x$测试集输入模型后对应的输出是$z_i(i=1,2,3)$,而Softmax要做的是利用以下公式计算样本$x$的后验概率$y_i=P(C_i|x)(i=1,2,3)$。后验概率的计算使用公式
$$ y_i= \frac{e^{z_1}} {\sum_{j=1}^3 e^{z_j}} $$
具体的计算过程如下。Softmax回归的过程简单描述为将样本$x$输入到各个判别器得到输出$z$作指数化(exponential),但由于指数化的结果可以是任意值,所以还要各个判别器指数化结果的归一化(Normalization)。
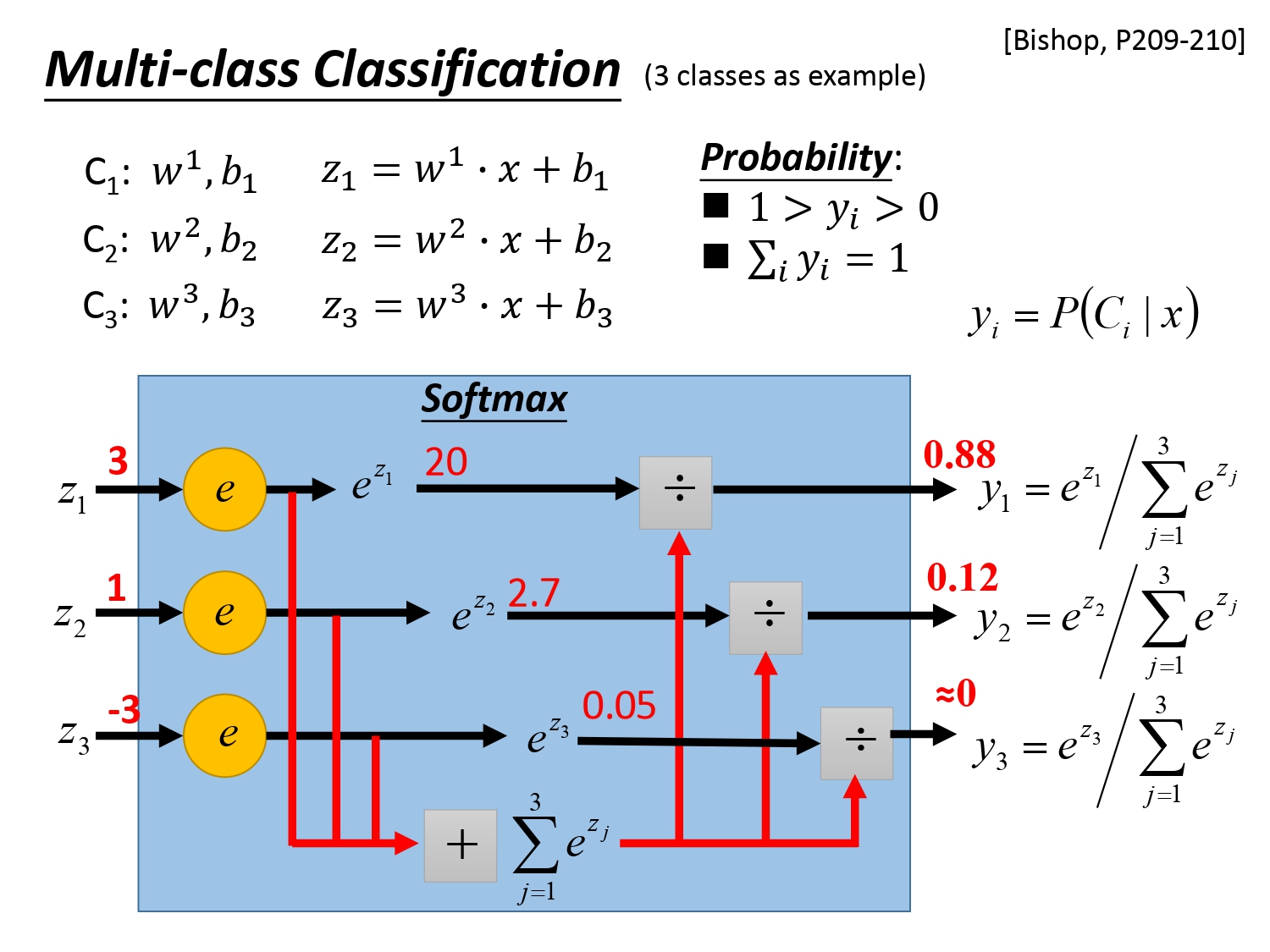
假设我们输入样本$x$经过线性回归模型后三个输出为$z_1=3,z_2=1.z_3=-3$,再经过Softmax回归处理,得到的结果是$y_1=0.88,y_2=0.12,y_3=0$,换句话说,Softmax回归的输出可以当作后验概率。
那为什么我们可以把Softmax回归的输出可以当作后验概率呢?
首先,我们可以像在Classification中一样,假设多个类别都服从高斯分布,然后让它们共享协方差矩阵$\Sigma$,再用最大似然估计的方法求得$\mu_1,\mu_2,\mu_3$,最后也能求得$y_1,y_2,y_3$。其次,在《信息论》中有个叫“最大熵”的概念,一样能推导出Softmax。(参考:指数簇分布的最大熵等价于其指数形式的最大似然界。二项式的最大熵解等价于二项式指数形式(sigmoid)的最大似然,多项式分布的最大熵等价于多项式分布指数形式(softmax)的最大似然,因此为什么用sigmoid函数,那是因为指数簇分布最大熵的特性的必然性。)
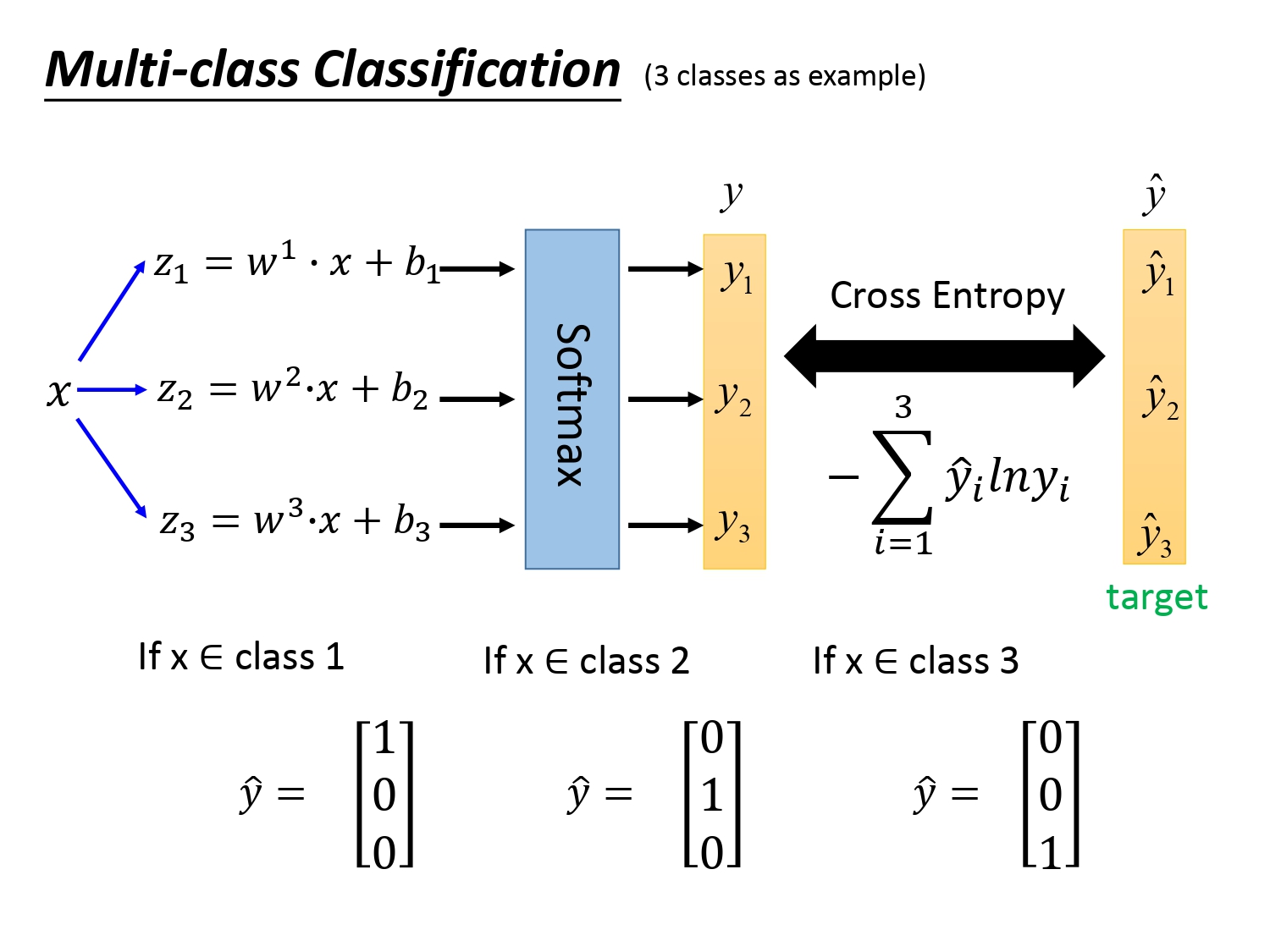
如下图所示,最后为避免使用数值1,2,3进行分类我们采用矩阵表示,再用多个变量的交叉熵作为损失函数去衡量目标值和预测值的差距。
逻辑回归的局限
其实逻辑回归处理分类问题有个非常强的局限,就是它根本没有办法将异或问题分类,如下图所示。
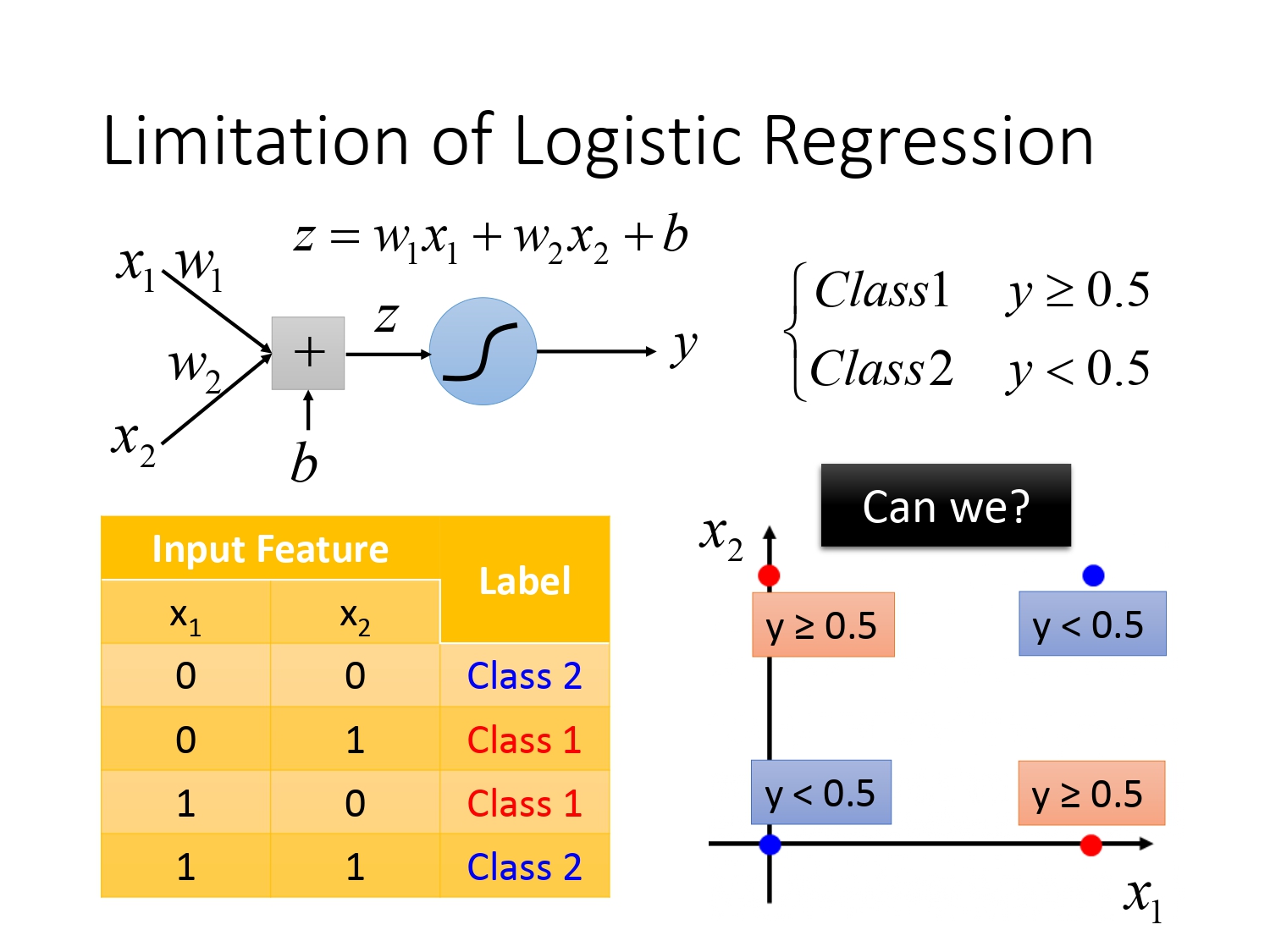
无论我们怎样去调整模型的权重$w_i$还是偏置$b$,模型仍是一条不能将二者区分开来的直线,如下图所示。
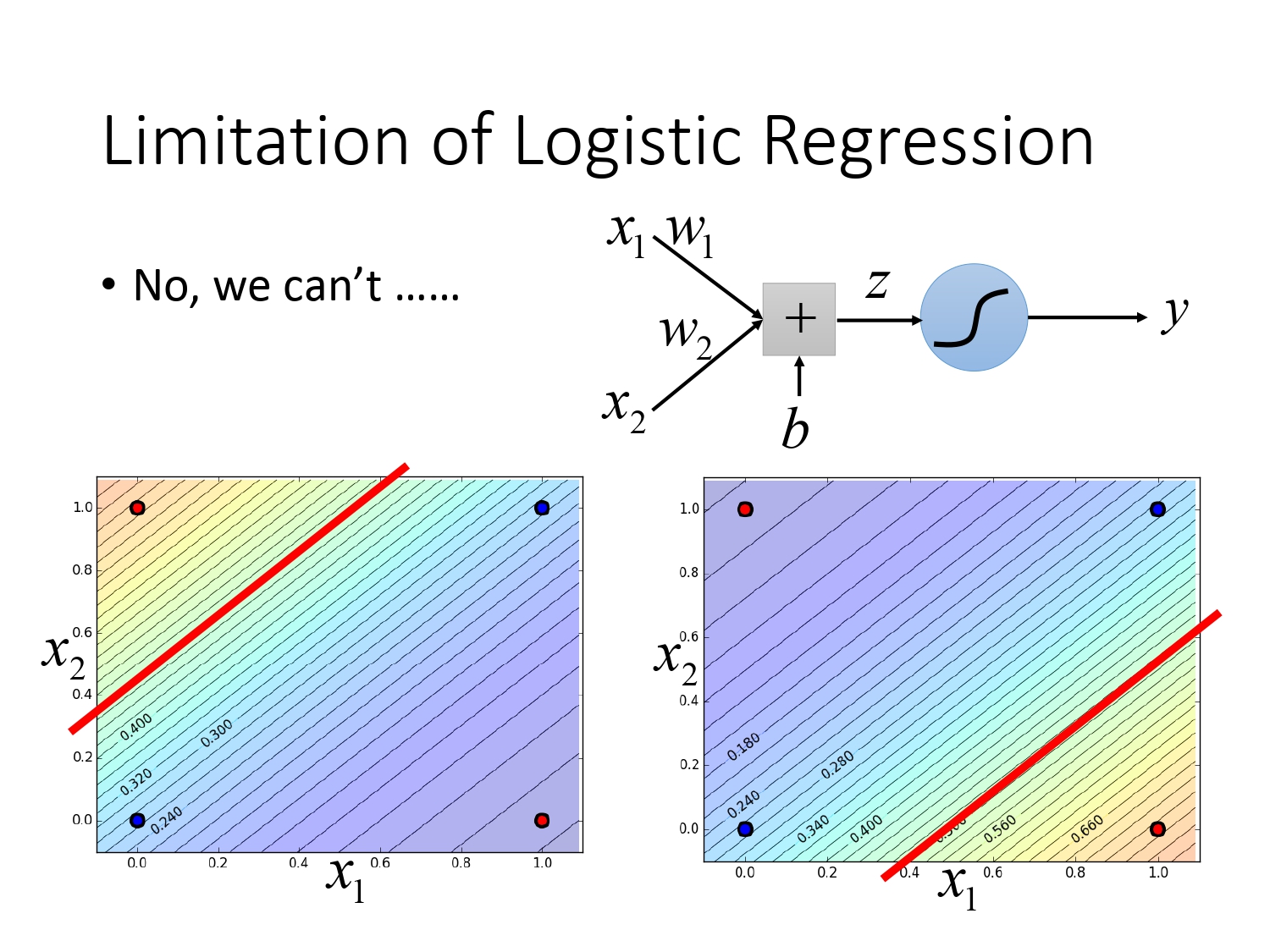
那我们应该怎么解决这个问题呢?
特征转换
异或问题难以分类的原因是分类的特征实在过于特殊,如果我们对原始特征进行特征转换(Feature Transformation)就能解决这个问题。特征转换的方法有很多种,对于上述01异或问题,可以将两个特征组成的平面$[x_1,x_2]^T$转化为新特征的平面$[x_1^\prime,x_2^\prime]^T$,其中$x_1^\prime$代表某点距离蓝点$[0,0]^T$的距离,$x_1^\prime$代表某点距离蓝点$[1,1]^T$的距离。所以对于$[x_1^\prime,x_2^\prime]^T$,$[1,1]^T$表示在原特征$x_1,x_2$的坐标平面中距离两个蓝点的距离都是1的点,也就是两个红点;对于原来的蓝点$[0,0]$,如果$x_1^\prime=0$,则$x_2^\prime=\sqrt{2}$,对于原来的蓝点$[1,1]$,如果$x_2^\prime=0$,则$x_1^\prime=\sqrt{2}$。
所以可以得到新平面下的两种类别点的分布,此时可以用逻辑回归将二者区分开来。
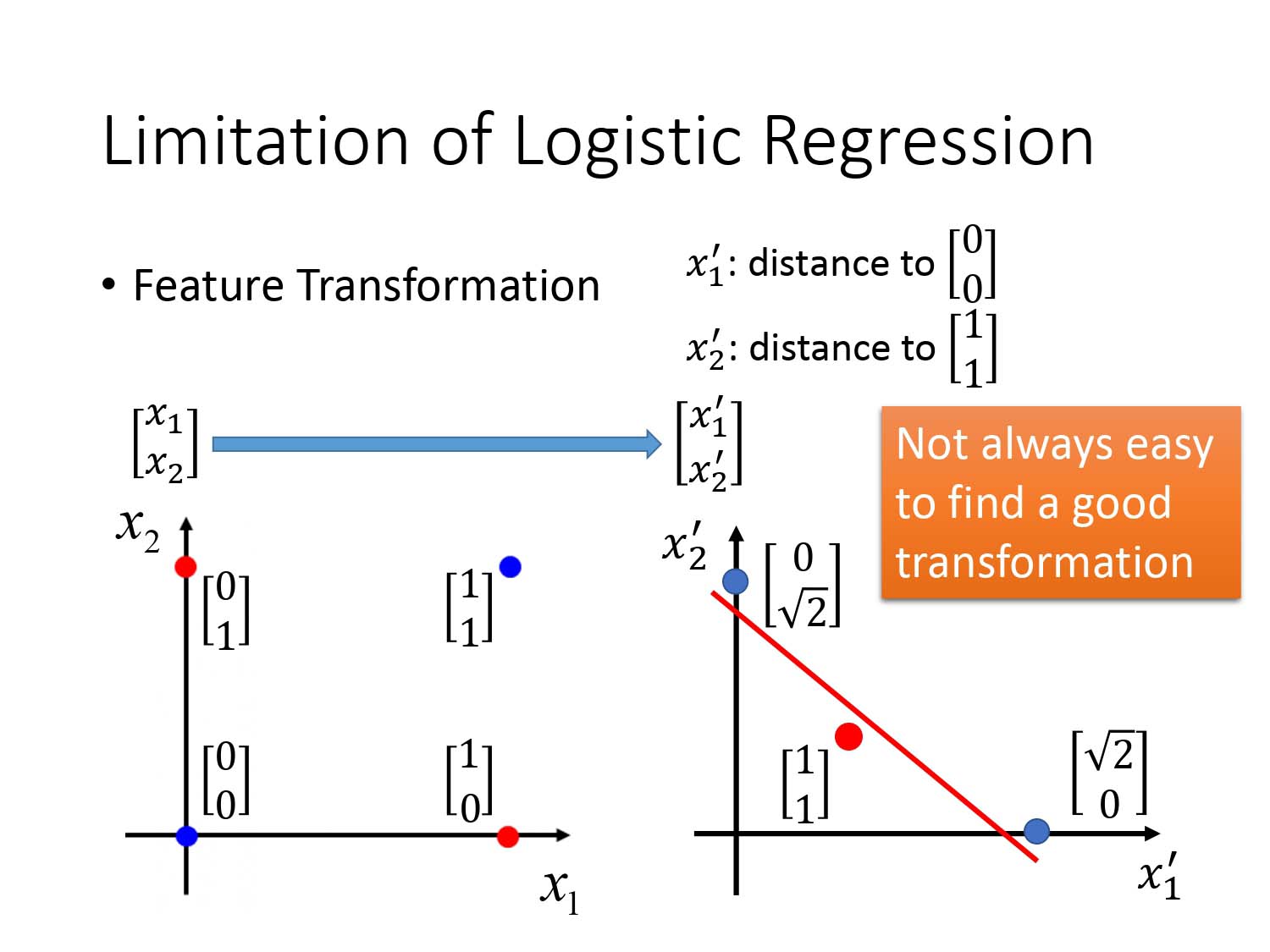
以上特征转换的方法只是针对上述的问题而已,但实际上我们不一定总能像刚刚那样找出一个好的特征转换。那怎么对不好的特征值进行特征转换呢?
级联逻辑回归模型
实际上我们可以通过级联多个逻辑回归模型进行特征转换,再通过最后一个逻辑回归模型进行分类。如下图所示。
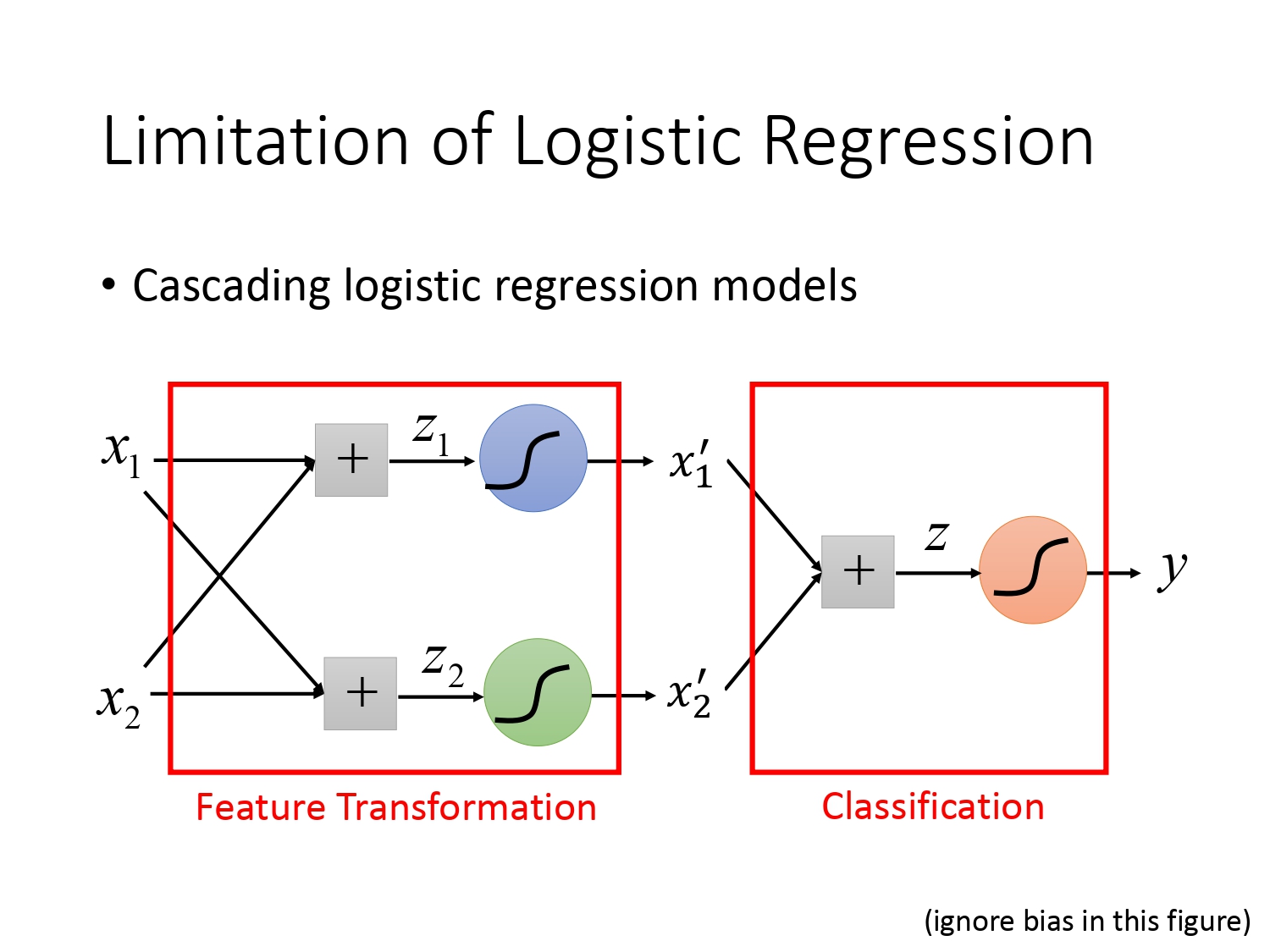
下面将以异或问题为例说明具体如何操作。假设我们有四个待分类异或样本,每个样本有两个特征$x_1,x_2$,我们要做的事是通过逻辑回归进行特征转换,将不利于分类的特征转换为利于分类的特征,再将利于分类的特征通过一个独立的逻辑回归进行分类。
在特征转换步骤中有$z_1=\omega_1x_1+\omega_2x_2+b_1$和$z_2=\omega_3x_1+\omega_4x_2+b_2$,得到$z_1,z_2$再输入$\sigma(z)$函数得到归一化后的新的特征$x^\prime_1$和$x^\prime_2$,我们得到的新的特征是可以通过逻辑回归进行分类的。
所以在分类步骤中先进行$z_3=\omega_5x_1^\prime+\omega_6x_2^\prime+b_3$,通过调整参数得到输出再输入$\sigma(z)$函数得到归一化后的输出$y$也就是后验概率,再根据后验概率是否大于0.5进行分类。如下图,通过调节权重和偏置的参数可以使得四个待分类样本的$x_1^\prime,x_2^\prime$值如下所示。
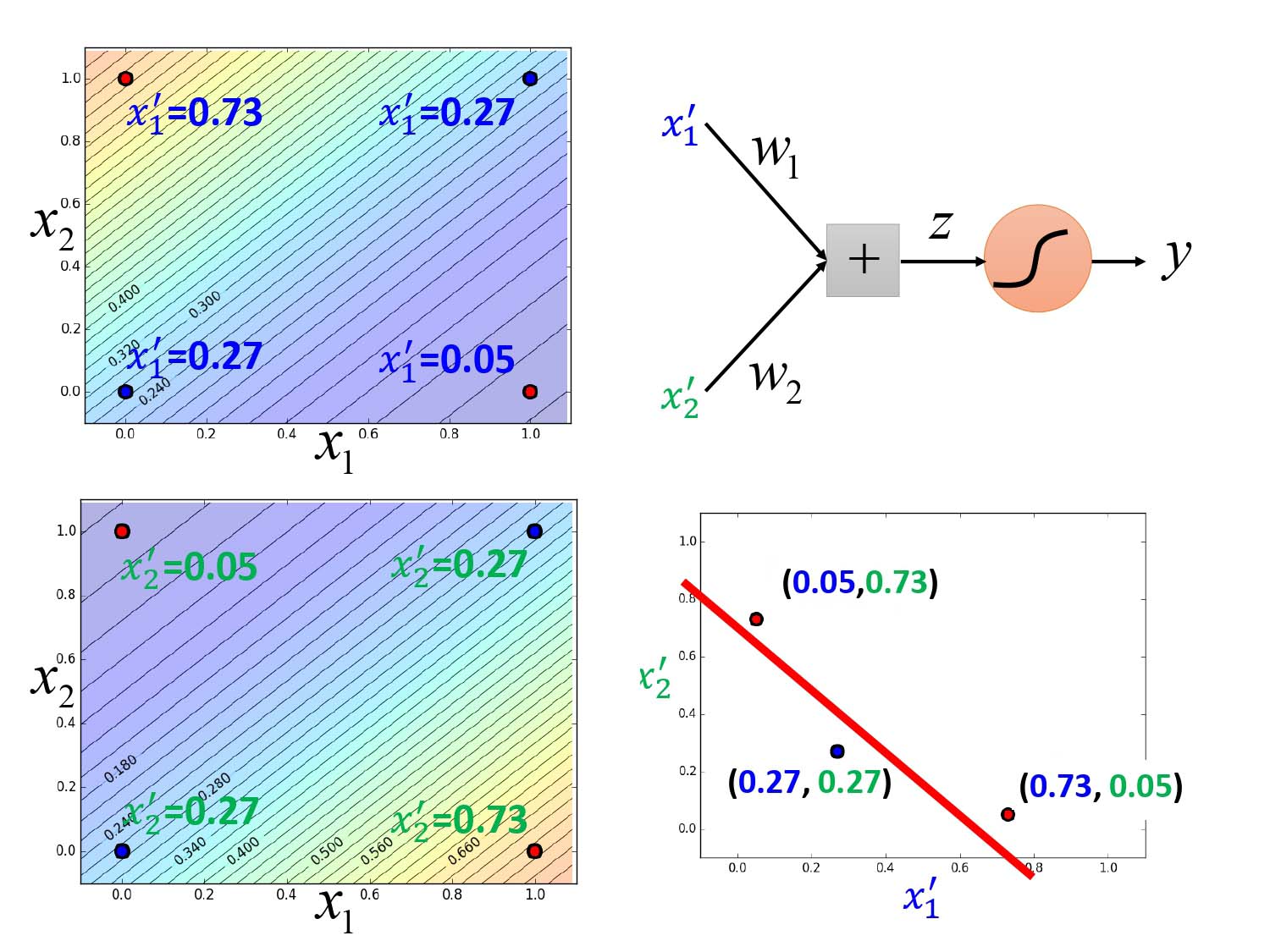
由上可见,一个逻辑回归的输入可以来自其他逻辑回归的输出,同时该逻辑回归的输出也可以作为其他逻辑回归的输入,组成的网络如下图所示。
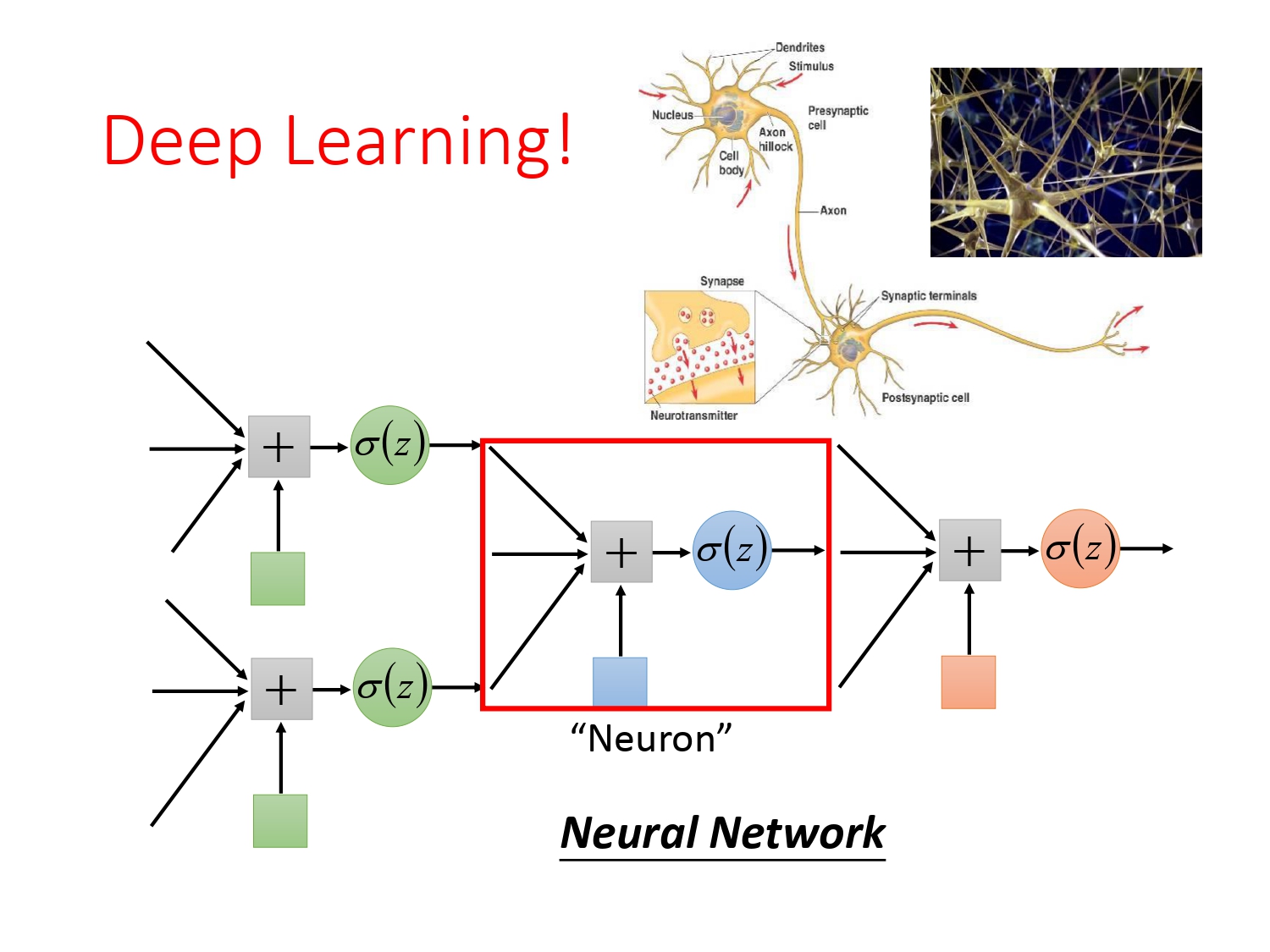
由多个逻辑回归组成的网络称为“类神经网络”(Neural Network),其中每个逻辑回归叫做神经元(Neural)。这就引出了以后要讲的深度学习(Deep Learning)。


